04_绝对值的意义与解题方法

遇见绝对值就分类法，95% 的问题都能解决！

绝对值有两种方法来理解，一种是代数意义，一种是几何意义。但推荐使用代数意义，几何意义有时候很难理解。

代表意义

代数意义

$|a|=\{\begin{array}{l}a,a>0\\ 0,a=0\\ -a,a<0\end{array}$

几何意义

表示线段长度。比如 $|x-4|>5$，表示点 x 到 4 的距离大于 5。

例题

1

已知 $|x-1|>4$，求 x 的取值范围。

解

先找出绝对值里的零点，有 x - 1 得出零点为 1。

然后再进行分类，

$\{\begin{array}{l}x-1>4,x\ge 1\\ 1-x>4,x<1\end{array}$

所以最终得出 $x>5$ 或 $x<-3$

2

解

3

求 $x^2-3|x|+2=0$ 的解。

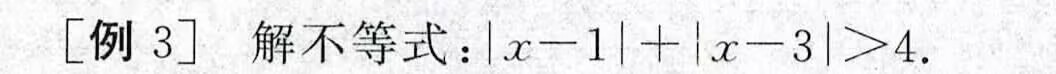
解

不要慌。按照分类的思想，很好求解。

零点就是 0，所以分 $x\ge 0$ 和 $x<0$ 两种情况。

$\{\begin{array}{l}x\ge 0\mathrm{时}，x^2-3x+2=0,\mathrm{所}\mathrm{以}x=1\mathrm{或}x=2\\ x<0\mathrm{时}，x^2+3x+2=0，\mathrm{所}\mathrm{以}x=-1\mathrm{或}x=-2\end{array}$

4

求 $x^2-3|x-2|-4=0$ 的解。

Details

$x-2=0$ 时 x 为 2，所以零点为 2。

1. $x\ge 2\mathrm{时}，x^2-3(x-2)-4=x^2-3x+2=0$

解得 $x=1$ 或 $x=2$，与一开始的条件取交集，得出 $x=2$

2. $x<2\mathrm{时}，x^2+3(x-2)-4=x^2+3x-10=0$

接的 $x=2\mathrm{或}-5$，与分类条件取交集，得出 $x=-5$

总和分类结果，得出 x = 2 或 -5