集合

06

解

余弦定理

C

07

解

正弦定理

D

08

解

余弦定理

A

09

解

排除法

D

10

解

余弦定理，面积公式

C

11

解

余弦定理，升降角公式

A

12

解

余弦正弦定理

$B$

13

解

正弦余弦定理

C

14

解

A

15 ~ 80

15

解

正弦定理

$B$

16

解

面积法。1 的代换

$9$

17

解，法一：余弦定理

余弦定理。

$\sqrt{3}-1$

解，法二：建系

$\sqrt{3}-1$

18

TIP

看见 $A<B<C$，可得出 $0<A<{60}^{\circ }$

证明：

$A+A+A<A+B+C={180}^{\circ }$

$A<{60}^{\circ }$

TIP

1. 知道了 $tan\theta$ 正切值，相当于已知了角

2. 求一个比值，可以随便设一个边长为 a，后面会约去的

3. 知道了 $tan\theta$，通过画一个直角三角形来算 $sin\theta ,cos\theta$，更直观、简单。

4. 最后要求的比值是 $\frac{BC}{BD}$，那么我们设未知数的时候就要设 BC 或 BD 为 x。而不用用其他边来表示 BC、BD，这就是经验！

   因为可能会导致其实没算错，但是表示得很复杂！

5. 几等分点公式

解

$D$

19

TIP

高数了底边，又告诉了高，90% 是要用面积公式！

方法：面积公式，余弦定理。

$\mathrm{h}⟶\mathrm{面}\mathrm{积}：\mathrm{底}\mathrm{乘}\mathrm{高}⟶\mathrm{底}\mathrm{有}\mathrm{了}⟶\mathrm{S}=\frac{\text{1}}{\text{2}}\times 8\times \mathrm{h}=4\mathrm{h}$

于是想到再找一个公式来表达面积，想到 $S=\frac{1}{2}absin\theta$

TIP

三边与外接圆半径公式：$S=\frac{abc}{4R}$

解，法一：面积公式

$S=\frac{1}{2}8\times h=4h$

$S=\frac{1}{2}\times 8\times asinB$

因为 $\frac{8}{sinC}=\frac{b}{sinB}=24=\frac{a}{sinA}$

所以 $a=24sinA$

$S=4asinB=4\times 24sinAsinB$

因为 $sin(A+B)=\frac{1}{3}$

$sin(A-B)=\frac{1}{4}$

所以 ${90}^{\circ }>A>B$

$cos(A-B)=\frac{\sqrt{15}}{4}$

$cos(A+B)=-cosC=-\frac{2\sqrt{2}}{3}$

$\{\begin{array}{l}cosAcosB+sinAsinB=\frac{\sqrt{15}}{4}\mathrm{①}\\ cosAcosB-sinAsinB=-\frac{2\sqrt{2}}{3}\mathrm{②}\end{array}$

$\mathrm{①}-\mathrm{②}$，得

$2sinAsinB=\frac{\sqrt{15}}{4}+\frac{2\sqrt{2}}{3}$

所以 $4h=4\times 24sinAsinB$

$h=12\times 2sinAsinB$

$=3\sqrt{15}+8\sqrt{2}$

20

TIP

通过正弦定理，把周长表示出来。

可以用角把周长表示出来。

然后确定 角的取值范围。

注意三个角的大小都要满足属于 $(0,{90}^{\circ })$，最后取交集！

TIP

在三角形中，$sin\theta$ 可以随便约去，因为 $sin\theta \in (0,\pi )$，

而 $cos\theta$ 不能随便约去，因为有可能 $\cos \theta =0$！

解

$C$

21

TIP

定弦定角问题。用初中的知识就可以解决。因为园中，定弦所对的圆心角的大小是固定的。

解

先根据条件，利用边角互换得出 $sinA=\frac{\sqrt{3}}{2},cosA=\frac{1}{2}$

然后根据 $S=\frac{1}{2}bc\frac{\sqrt{3}}{2}$

$=\frac{\sqrt{3}}{4}bc$

接下来就是算 bc 的最大值，

利用余弦定理，有

$bc=b^2+c^2-4⩾2bc-4$

$bc⩽4$

所 $S_m=\sqrt{3}$

$D$

22

解

首先将要求的东西变形，可以得到要求的是 $tanB+tanC$ 的最小值。

那么根据条件，$\frac{2b}{cosB}=\frac{a}{cosA}+\frac{c}{cosC}$

$2tanB=tanA+tanC$

所以 $tanA=2tanB-tanC$

又因为正切公式 $tanA+tanB+tanC=tanAtanBtanC$

所以 $3tanB=(2tanB-tanC)tanBtanC$

$3=(2tanB-tanC)tanC$

$tanB=\frac{3}{2tanC}+\frac{1}{2}tanC$

$\omega =tanB+tanC$

$=\frac{3}{2tanC}+\frac{3}{2}tanC⩾2\sqrt{\frac{9}{4}}=3$

$A$

23

TIP

根据题目等式条件，可以得出 $2R=\frac{a}{sinA}=1=\frac{c}{sinC}$

解下来，求 $a+b$，转化为求 $sinA+sinC$

$=sinA+sin(B+A)$

解 法一

$B$ 是已知的，

$\omega =sinA+sin(\frac{\pi }{6}+A)$

$=\frac{3}{2}sinA+\frac{\sqrt{3}}{2}cosA$

$=\sqrt{\frac{9}{4}+\frac{3}{4}}sin(A+\phi )$

$tan\phi =\frac{\sqrt{3}}{3},\phi =\frac{\pi }{6}$

$0<A<\frac{2\pi }{3}$

$\frac{\pi }{6}<A+\phi <\frac{5\pi }{6}$

$\omega =\sqrt{3}\theta ,\theta \in (\frac{\pi }{6},\frac{5\pi }{6})$

$A$

解，也可以根据 $sinB=b=\frac{\sqrt{3}}{2}$，用圆的定弦角来解决问题

24

TIP

若题目求一个比值，且这个比值为定值，那么有 3 种可能：

1. 需要用一个变量来表示分子、分母，最后这个变量可以被约去
2. 根据条件得到一个关于这个变量等式，解出这个变量
3. 根据条件得到一个关于这个变量等式，但不能通过解方程的形式解出这个变量；要通过不等式放缩，比如左边式子的最大值等于右边式子的最小值，那么得出左边式子等于它的最大值，右边式子等于它的最小值。

TIP

解三角形中，看到有很多平方项，80% 要用到余弦定理。

解

$3b^2+2c^2=a^2+2bcsinA$

必须留 sinA，否则后面用不了均值不等式，因为有 3 项。我们只需要两项。

$3b^2+2c^2-a^2=2bcsinA$

$b^2+c^2-a^2+2b^2+c^2=2bcsinA$

$cosA+\frac{2b^2+c^2}{2bc}=sinA$

$\frac{b}{c}+\frac{c}{2b}=sinA-cosA=\sqrt{2}sin(A-\frac{\pi }{4})⩽\sqrt{2}$

而 $\frac{b}{c}+\frac{c}{2b}⩾2\sqrt{\frac{1}{2}}=\sqrt{2}$

所以 左边的最大值等于右边的最小值

所以 $\frac{b}{c}=\frac{c}{2b},A-\frac{\pi }{4}=\frac{\pi }{2}$

$A=\frac{3\pi }{4}$

$\frac{S}{b^2}=\frac{1}{2}\frac{bcsinA}{b^2}$

$=\frac{1}{2}\frac{c}{b}sinA$

$=\frac{1}{2}\frac{c}{b}\frac{\sqrt{2}}{2}$

$=\frac{1}{2}$

$B$

25

对偶式

既出现 $sinA,cosA$ 和一个数的时候，用对偶式求 $sinA,cosA$ 超级快速简便！

但注意对偶式的用法：新的对偶式 sin、cos 交叉互变，中间的符号取反，右边令为 t。

比如有 $sinA+2cosA=2$，

那么我们的对偶式为 $cosA-2sinA=t$，

注意不是 $sinA-2cosA=t$！！

然后两边同平方，相加即可接出 $sinA,cosA$。

对偶式补充：比对偶式更简单的方法

直接将 正弦移到式子的一边，然后式子两边平方，再全部化为余弦，求余弦的值。

TIP

三角函数中通过角求正弦、余弦、正切的范围，要注意角的定义域在同一个单调区间。否则比不了。

两角互余结论

两角互余，说明 ${\theta }_1+{\theta }_2={90}^{\circ }$

当三角形是锐角三角形，且有一个角比如 A 是定角 $A$ 时，那么我们是可以求出另外两个角的正弦、余弦、正切范围的，且这两个角的范围是相同的。

并且不一定是非要知道 A 的大小，知道了 A 的正弦、余弦、正切就相当于知道了角的大小了。

比如已知 $sinA=\frac{4}{5},cosA=\frac{3}{5}$，且三角形为锐角三角形，那么

$0<B=\pi -A-C<\frac{\pi }{2}$

$0<C<\frac{\pi }{2}$

所以

$\frac{\pi }{2}<A+C<\pi$

$\frac{\pi }{2}-A<C<\frac{\pi }{2}<\pi -A$

所以 $1>sinC>sin(\frac{\pi }{2}-A)=cosA=\frac{3}{5}$

$+\mathrm{\infty }>tanC>tan(\frac{\pi }{2}-A)=\frac{1}{tanA}=\frac{3}{4}$

$0<cosC<cos(\frac{\pi }{2}-A)=sinA=\frac{4}{5}$

B 的正弦、余弦、正切范围同理！

TIP

$\frac{3}{5}<\frac{\sqrt{2}}{2}$

重做

解

$a^2=2S+b^2+c^2-2bc$

$a^2=b^2+c^2-2bccosA$

上式 - 下式，

$0=2S+2bccosA-2bc$

$0=bcsinA+2bccosA-2bc$

$sinA+2cosA=2$

$\{\begin{array}{l}sinA+2cosA=2\\ cosA-2sinA=t\end{array}$

$1+4=t^2+4$

$t=1,-1$

当 $t=1,$

经算不符题意，

$t=-1$

$sinA=\frac{4}{5},cosA=\frac{3}{5}$

$\omega =\frac{2b^2+c^2}{bc}$

$=\frac{2b}{c}+\frac{c}{b}$

令 $\frac{b}{c}=t,\omega =2t+\frac{1}{t}$

$t=\frac{sinB}{sinC}$

$=\frac{4}{5tanC}+\frac{3}{5}$

$0<B<\frac{\pi }{2}$

$\frac{\pi }{2}<A+C<\pi$

$\frac{\pi }{2}-A<C<\frac{\pi }{2}$

$tan\frac{\pi }{2}>tanC>tan(\frac{\pi }{2}-A)=\frac{1}{tanA}=\frac{3}{4}$

所以 $\frac{5}{3}>t>\frac{3}{5}$

所以根据对钩函数图像

$\omega \in [\sqrt{2}+\sqrt{2},\frac{10}{3}+\frac{3}{5})$

$\in [2\sqrt{2},\frac{59}{15})$

$C$

26

错误解答

设 $OA=x$，则 $AP=2-x$，且 $AB=AP=2-x$

又因为做弦 BC 的中垂线，一定过圆心 O 点，所以 $OA=OD$，三角形 OAD 是等边三角形。

所以 $S=x(2-x),x\in (0,2)$

所以 $S_{max}=1$

错误原因： 以 AP 为半径作圆，会与圆 O 相切，这也就说明了 $AB>AP$，所以错了。

解

如图，

$S=(2cos\theta -2\sqrt{3}sin\theta )4sin\theta$

$=8(sin\theta cos\theta -\sqrt{3}si{n}^2\theta )$

$=8(\frac{1}{2}sin2\theta -\sqrt{3}\frac{1-cos2\theta }{2})$

$=4sin2\theta -4\sqrt{3}(1-cos2\theta )$

$=4sin2\theta +4\sqrt{3}cos2\theta -4\sqrt{3}$

$=4(2sin(2\theta +\frac{\pi }{3}))-4\sqrt{3}$

当 $2\theta +\frac{\pi }{3}=\frac{\pi }{2}$

$\theta =\frac{\pi }{12}$ 时，

$S_{max}=8-4\sqrt{3}$

27

TIP

题目说表达式有最大值，那就求表达式的最大值。

如果定义域是开区间，那么最大值一定在开区间的中间取得，这就会对开区间的值有一定取值范围要求，

据此来求出我们要求的式子的取值范围。

而不是通过均值不等式一步得出最大值。

解

根据正弦定理，

$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}=\frac{b}{sinB}=\frac{c}{sinC}=2$

$B=\frac{\pi }{3}-C$

$b=2sin(\frac{\pi }{3}-C)$

$c=2sinC$

$mb+nc=2msin(\frac{\pi }{3}-C)+2nsinC$

$=2m[\frac{\sqrt{3}}{2}cosC-\frac{1}{2}sinC]+2nsinC$

$=\sqrt{3}mcosC-msinC+2nsinC$

$=\sqrt{3}mcosC+(2n-m)sinC$

$=\sqrt{3m^2+(2n-m{)}^2}sin(\phi +C)$

$tan\phi =\frac{\sqrt{3}m}{2n-m}$

因为 $C\in (0,\frac{\pi }{3})$

$\phi +C\in (\phi ,\phi +\frac{\pi }{3})$

$\frac{\pi }{6}<\phi <\frac{\pi }{2}$

$\frac{\sqrt{3}}{3}<tan\phi$

所以 令 $t=\frac{n}{m}$

$\frac{1}{2t-1}>\frac{1}{3}$

$\frac{3}{3(2t-1)}>\frac{2t-1}{3(2t-1)}$

$\frac{3-2t+1}{3(2t-1)}>0$

$\frac{4-2t}{3(2t-1)}>0$

$\frac{2-t}{2t-1}>0$

$t\in (\frac{1}{2},2)$

28

TIP

满足三角形的三边条件：$a>b,a>c,\mathrm{且}b+c>a$

解

$a{x}^2-bx+c=0$

$a+b=\frac{b}{a},a=b(\frac{1}{a}-1)$

$a=b\frac{1-a}{a}$

$b=\frac{a^2}{1-a}$

又 $ab=\frac{c}{a}$

$c=a^{2}b=\frac{a^4}{1-a}$

$\omega =a+b-c=a+\frac{a^2}{1-a}-\frac{a^4}{1-a}$

$=a+\frac{a^4-a^2}{a-1}=a+\frac{a^2(a^2-1)}{a-1}$

$ = a + a^2(a+1) = a^3 + a^2 + a$

因为 $b=\frac{a^2}{1-a}>0$

所以 $0<a<1$

$c=\frac{a^4}{1-a}>0$

$0<a<1$

因为 $a<b=\frac{a^2}{1-a}$

所以 $1<\frac{a}{1-a},$

$1-a<a$

$\frac{1}{2}<a<1$

因为 $a+c>b$

所以 $a+\frac{a^4}{1-a}>\frac{a^2}{1-a}$

$1+\frac{a^3}{1-a}>\frac{a}{1-a}$

$\frac{1-a+a^3-a}{1-a}>0$

$a^3-2a+1>0$

$(a-1)(a^2+a-1)>0$

所以 $a^2+a-1<0$

所以 $\frac{-1-\sqrt{5}}{2}<a<\frac{-1+\sqrt{5}}{2}$

所以 $\frac{1}{2}<a<\frac{\sqrt{5}-1}{2}$

$\omega (\frac{1}{2})=\frac{1}{8}+\frac{2}{8}+\frac{4}{8}=\frac{7}{8}$

令 $\frac{\sqrt{5}-1}{2}=t,t^2+t-1=0$

$\omega (\frac{\sqrt{5}-1}{2})=t^3+t^2+t=t^3+t^2-t+2t=2t=\sqrt{5}-1$

所以 $\omega \in (\frac{7}{8},\sqrt{5}-1)$

29

TIP

正弦定理，边角互换。得出 $A,B,C$ 之间的关系。

解

$cosC=\frac{sinB-sinA}{2sinA}$

$2sinAcosC=sinB-sinA$

$=sin(A+C)-sinA$

$=sinAcosC+cosAsinC-sinA$

$sinAcosC-cosAsinC=-sinA$

$sinA=sin(C-A)$

所以 $A=C-A$ 或 $C=\pi (\mathrm{舍})$

$\omega =sin(A+C)+sinA$

$=sinAcosC+cosAsinC+sinA$

$=sinAcos2A+cosAsin2A+sinA$

$=sinA(1-2si{n}^{2}A)+2sinAco{s}^{2}A+sinA$

$=sinA-2si{n}^{3}A+2sinA(1-si{n}^{2}A)+sinA$

$=4sinA-4si{n}^{3}A$

$sinA=t,$

$\omega =4t-4t^3$

$0<C=2A<\frac{\pi }{2},0<A<\frac{\pi }{4}$

$0<B=\pi -A-2A=\pi -3A<\frac{\pi }{2}$

$\frac{\pi }{6}<A<\frac{\pi }{3}$

$0<A<\frac{\pi }{2}$

$\frac{\pi }{6}<A<\frac{\pi }{4}$

$\frac{1}{2}<sinA<\frac{\sqrt{2}}{2}$

$f(t)=4t-4t^3$

$f^{\prime }(t)=4-12t^2=4(1-3t^2)$

$f(t)$ 在 $(\frac{1}{2},\frac{\sqrt{3}}{3})\uparrow ,(\frac{\sqrt{3}}{3},\frac{\sqrt{2}}{2})\downarrow$

$f(t{)}_{max}=f(\frac{\sqrt{3}}{3})=\frac{8\sqrt{3}}{8}$

$D$

30

TIP

三角形中，看到两个角互为补角，那么可以用两次余弦定理，两个余弦定理相加 = 0

解

将 $sin$ 的关系放到同一个三角形中，那么 $sinADB=3sinBAC$

$AB=3BD$

设 $BD=y,AB=3y$

$\mathrm{表}\mathrm{达}\mathrm{式}=3x^2\frac{9x^2+x^2-9y^2}{2\cdot 3x^2}-3y$

$=\frac{10x^2-9y^2}{2}-3y$

$=5x^2-\frac{9}{2}{y}^2-3y$

用两次余弦定理：

$\frac{x^2+y^2-x^2}{2xy}+\frac{4x^2+y^2-9y^2}{2\cdot 2xy}=0$

$2x^2=3y^2$

所以 $\mathrm{式}\mathrm{子}=3y^2-3y$，当 $y=\frac{1}{2}$ 时取得最大值。

所以 $cosC=\frac{x^2+x^2-y^2}{2x^2}=\frac{2x^2-y^2}{2x^2}=1-\frac{y^2}{3y^2}=\frac{2}{3}$

$sinC=\frac{\sqrt{5}}{3}$

$x=\sqrt{\frac{3}{2}}y=\frac{\sqrt{6}}{4}$

$AC=3x=\frac{3\sqrt{6}}{4}$

$BC=\frac{\sqrt{6}}{4}$

$S=\frac{1}{2}\times \frac{3\sqrt{6}}{4}\times \frac{\sqrt{6}}{4}\times \frac{\sqrt{5}}{3}$

$=\frac{1}{2}\times \frac{6\sqrt{5}}{16}=\frac{3\sqrt{5}}{16}$

$D$

31

解

$cosB=bcosC$

$\frac{9+4-b^2}{12}=b\frac{b^2+4-9}{4b}$

可解得 $b=\sqrt{7}$

所以 $cosB=\frac{9+4-7}{12}=\frac{1}{2}$

因为面积一半，所以

$PB=x,BQ=y$

$\frac{1}{2}sinBxy=\frac{1}{2}sinB6-\frac{1}{2}sinBxy$

$xy=3$

$PQ=\sqrt{x^2+y^2-2xy\frac{1}{2}}$

$=\sqrt{x^2+y^2-xy}$

$⩾\sqrt{xy}$

$=\sqrt{3}$，当 $x=y=\sqrt{3}$ 时取等。

32

TIP

阿氏圆

解

$\frac{S_{ABD}}{S_{AEC}}=\frac{BD}{CE}=\frac{AB\cdot AD}{AE\cdot AC}$

$\frac{S_{ABE}}{S_{ACD}}=\frac{BE}{CD}=\frac{AB\cdot AE}{AD\cdot AC}$

上式乘下式，

$\frac{BD\cdot BE}{CD\cdot CE}=\frac{A{B}^2}{A{C}^2}=\frac{1}{4}$

$\frac{AB}{AC}=\frac{1}{2}$

$AC=2AB$

$A(x,y)$

$B(0,0),C(3,0)$

所以 $AC=\sqrt{(x-3{)}^2+y^2}$

$AB=\sqrt{x^2+y^2}$

$\sqrt{(x-3{)}^2+y^2}=2\sqrt{x^2+y^2}$

$(x-3{)}^2+y^2=4x^2+4y^2$

$3x^2+3y^2+6x-9=0$

$(x+1{)}^2+y^2=4$

所以 A 点轨迹是一个圆，称为阿氏圆

相切时，角 A 最大

$AC=2\sqrt{3}$

$S=\frac{1}{2}\times 2\times 2\sqrt{3}=2\sqrt{3}=\frac{1}{2}\cdot 4h$

$h=\sqrt{3}$

$S_{ABC}=\frac{1}{2}\times 3\times \sqrt{3}$

$=\frac{3\sqrt{3}}{2}$

33

TIP

不能统一变量，因为没有任何统一变量的条件

开区间取最值，一定在极值点处取

组元法

因为三个角，不论再怎么化简，也还有 2 个角。

所以像这种多变量求最值，如果最终不能用一个变量表示，那么可以假设其中一个变量为常数，求关于另一个变量的最值。

这种最值一般就是化简得出三角函数的振幅。因为三角函数的最值不会是无穷大，一定在振幅处取得。

解

$\omega =cosA(3sinB+4sinC)$

求最小值，那么 $cosA<0,\frac{\pi }{2}<A<\pi ,cosA\in (-1,0)$

因为三角形中 $sin$ 一定大于 0！$cos$ 有正有负！

把 A 看作常数，求 $3sinB+4sinC$ 的最大值。

$3sin(A+C)+4sinC$

$=3sinAcosC+3cosAsinC+4sinC$

$=3sinAcosC+(3cosA+4)sinC$

$=\sqrt{9si{n}^{2}A+(3cosA+4{)}^2}sin(\phi +C)$

最大值为 $\sqrt{9si{n}^{2}A+9co{s}^{2}A+24cosA+16}$

$=\sqrt{25+24cosA}$

$\omega =cosA\sqrt{25+24cosA}$

令 $\sqrt{25+24cosA}=t,t\in (1,5)$

$cosA=\frac{t^2-25}{24}$

$\omega =\frac{t^2-25}{24}t=\frac{t^3-25t}{24}$

${\omega }^{\prime }=\frac{1}{24}(3t^2-25)$

${\omega }_{min}=\omega (\frac{5}{\sqrt{3}})$

$=\frac{1}{24}(\frac{25}{3}\frac{5}{\sqrt{3}}-25\frac{5}{\sqrt{3}})$

$=-\frac{125\sqrt{3}}{108}$

34

TIP

提示：万能公式。

挺难算的。

$sin2\theta =\frac{2tan\theta }{1+ta{n}^2\theta }=\frac{2sin\theta cos\theta }{1}$

$cos2\theta =\frac{1-ta{n}^2\theta }{1+ta{n}^2\theta }=\frac{co{s}^2\theta -si{n}^2\theta }{1}$

$tan\theta =\frac{2tan\theta }{1-ta{n}^2\theta }=\frac{2sin\theta cos\theta }{cos2\theta }$

解

根据题目条件，得出 $\mathrm{\angle }C=2\mathrm{\angle }A$

所以 $BC=\frac{1}{cos\theta }$

$S=\frac{1}{2}2\frac{1}{cos\theta }\cdot sin3\theta$

$=\frac{sin3\theta }{cos\theta }$

$=\frac{sin2\theta cos\theta +cos2\theta sin\theta }{cos\theta }$

$=sin2\theta +cos2\theta tan\theta$

$=\frac{2tan\theta }{1+ta{n}^2\theta }+\frac{1-ta{n}^2\theta }{1+ta{n}^2\theta }tan\theta$

令 $tan\theta =t,t\in (1,\sqrt{3})$

$S=\frac{2t}{1+t^2}+\frac{t-t^3}{1+t^2}$

$=\frac{3t-t^3}{1+t^2}$

$S^{\prime }=\frac{(3-3t^2)(1+t^2)-(3t-t^3)2t}{(1+t^2{)}^2}$

$=\frac{-t^4-6t^2+3}{(1+t^2{)}^2}$

$t^2=\frac{6\pm \sqrt{36+12}}{-2}$

$t^2=\pm 2\sqrt{3}-3$

当 $t^2=2\sqrt{3}-3$ 时，S 取最大值

$cos2\theta =\frac{1-ta{n}^2\theta }{1+ta{n}^2\theta }$

$=\frac{1-t^2}{1+t^2}$

$=\frac{4-2\sqrt{3}}{2\sqrt{3}-2}$

$=\frac{\sqrt{3}-1}{2}$

35

TIP

利用正弦定理，余弦定理完成边角互换，再结合基本不等式，即可判断 A，B 在锐角三角形 ABC 中的关系。

利用正切恒等式

$tanAtanBtanC=tanA+tanB+tanC$，再结合 $tanB=3tanC$ 和基本不等式即可判断 C。利用向量数量积的运算来判断 D。

有点太难了。

解

对于 A，$tanB=3tanC$，则 $\frac{sinB}{cosB}=3\frac{sinC}{cosC}$，即 $sinBcosC=3cosBsinC$

所以 $sinBcosC+cosBsinC=4cosBsinC$，即 $sin(B+C)=4cosBsinC$

又 $A+B+C=\pi$，所以 $sinA=sin(B+C)=4cosBsinC$

对于 D，过 B 作 $BD\perp AC$，则 $CD=BCcosC=acosC$

又 P 在 CD 间运动时，$\overrightarrow{PB}$ 与 $\overrightarrow{PC}$ 的夹角为钝角，因此要求 $\overrightarrow{PB}\cdot \overrightarrow{PC}$ 的最小值，P 应在 CD 之间运动，即 $|\overrightarrow{CP}|\in (0,acosC)$，

又 $\overrightarrow{PB}\cdot \overrightarrow{PC}=(\overrightarrow{CB}-\overrightarrow{CP})(-\overrightarrow{CP})=|CP{|}^2-|CP|acosC$

当 $|CP|=\frac{acosC}{2}$ 时，$\overrightarrow{PB}\cdot \overrightarrow{PC}$ 取最小值为 $-\frac{1}{4}{a}^{2}co{s}^{2}C$，故 D 错误。

$C$

36

解

37

解

38

解

39

解

【点睛】关键点点睛：本题考查三角形中的最值与范围问题，主要思考方向有两个，一个是借助余弦定理得到边之间的关系，从而通过基本不等式求解，一个是借助正弦定理将边化为角，通过三角形中角的关系将多个变量角化为单变量，借助函数性质得到范围或最值.

40

解

41

解

42

解

43

TIP

小心，辅助角公式的辅助角大小范围一定属于 $(-\frac{\pi }{2},\frac{\pi }{2})$！

比如，$cos2A-\sqrt{3}sin2A=cos2B-\sqrt{3}2B$

那么 $2sin(\frac{\pi }{6}-2A)=2sin(\frac{\pi }{6}-2B)$

而不是 $2sin(\frac{5\pi }{6}-2A)=2sin(\frac{5\pi }{6}-2B)$！！

如果是 $\frac{5\pi }{6}$ 自己带进去算一下也会发现是错的。

TIP

一般来讲，在三角形 ABC 中，如果 $sin(\phi -A)=sin(\phi -B)$，我们都会化成

$sin(A-\phi )=sin(B-\phi )$，让角的系数变为正数。

然后得出结论 $A-\phi =B-\phi$

或 $A-\phi +B-\phi =\pi$。

解（1）

$co{s}^{2}A-co{s}^{2}B=\frac{\sqrt{3}}{2}sin2A-\frac{\sqrt{3}}{2}sin2B$

$\frac{cos2A+1}{2}-\frac{cos2B+1}{2}=\frac{\sqrt{3}}{2}sin2A-\frac{\sqrt{3}}{2}sin2B$

$cos2A-cos2B=\sqrt{3}sin2A-\sqrt{3}sin2B$

$cos2A-\sqrt{3}sin2A=cos2B-\sqrt{3}sin2B$

$sin(\frac{\pi }{6}-2A)=sin(\phi -2B)$

因为 $A+B\in (0,\pi )$

$sin(2A-\frac{\pi }{6})=sin(2B-\frac{\pi }{6})$

$2A-\frac{2\pi }{6}+2B=\pi$

$A+B=\frac{2\pi }{3}$

$C=\frac{\pi }{3}$

解（2）

$sinC=\frac{\sqrt{3}}{2}$

$a=2\times \frac{4}{5}=\frac{8}{5}$

$S=\frac{1}{2}acsinB=\frac{1}{2}\frac{8}{5}\sqrt{3}sin(A+C)$

$=\frac{4\sqrt{3}}{5}(\frac{4}{5}\frac{1}{2}+\frac{3}{5}\times \frac{\sqrt{3}}{2})$

$=\frac{8\sqrt{3}+18}{25}$

44

TIP

• 知道两个角，和两条边，可以使用射影定理。
• 在三角形中，$sinA,sinB,sinC$ 一定不会为 0，只有 $cosA,cosB,cosC$ 需要小心为零！！

解

45~46

TIP

注意，$cos\frac{\pi }{6}=\frac{\sqrt{3}}{2}$，不是 $sin\frac{\pi }{6}=\frac{1}{2}$，

只有 $sin\frac{\pi }{4}=\frac{\sqrt{2}}{2}$ 才会出现 $\sqrt{2}$ ！

45 题，解

46 题，解

47

TIP

在三角形中，知道了 $sinA=3cosA$，即知道了 $tanA=3$

是可以直接求出 $sinA,cosA$ 的，因为 $A$ 一定属于 $(0,\frac{\pi }{2})$，

所以可以画一个三角形，得出 $sinA,cosA$ 的值。

解

48

解

49

TIP

$\sqrt{63}=\sqrt{7\times 9}$ 是可以化简的。

解

50

解

51

TIP

当我们得到关于 3 个变量的等式，却好像找不到其他关系式可以把 3 个变量的式子变成 2 个变量的式子，可能这个式子可以通过因式分解，得出两个因式其中一个一定为 0。

这样就通过一个包含 3 个变量的等式得出 一个关于 2 个变量的等式。这种思想很常见！

比如：$33ac=9c^2+18a^2$

那么 $11ac=3c^2+6a^2$

$6a^2-11ac+3c^2=0$

$(2a-3c)(3a-c)=0$

那么 $a=\frac{3}{2}$ 或 $a=\frac{c}{3}$

解

52

TIP

如果锐角三角形中有 $A+B=\frac{2\pi }{3}$，那么

对于 $A$，有

$\{\begin{array}{l}0<A<\frac{\pi }{2}\\ 0<C=\frac{2\pi }{3}-A<\frac{\pi }{2}\end{array}$

解得 $A\in (\frac{\pi }{6},\frac{\pi }{2})$

如果不是锐角三角形，那么范围就是 $A\in (\frac{\pi }{6},\frac{2\pi }{3})$

解

53

解

选择条件 1.

54

解

55

解

56

解

57

解

诱导公式的逆用

• 在三角形中，若 $sinB=-cosC$，则 $sinB=sin(C-\frac{\pi }{2})=-cosC$

则 $\frac{\pi }{2}<C<\pi ,0<B<\frac{\pi }{2}$

且 $B=C-\frac{\pi }{2}$

TIP

记住，看到 $1+cos2B$，要知道它是等于 $1+2co{s}^{2}B-1=2co{s}^{2}B$ 的。可以把 1 给约去。

TIP

有时候需要给出的条件需要化到最简形式，以得出角之间的关系，不然第二问做不出来。

58

解

TIP

$\sqrt{2}$ 别抄成 $\sqrt{7}$ 了！

59

解

60

解

TIP

不同问的条件不同，作图时一定要把上问的条件替换掉。

61

解

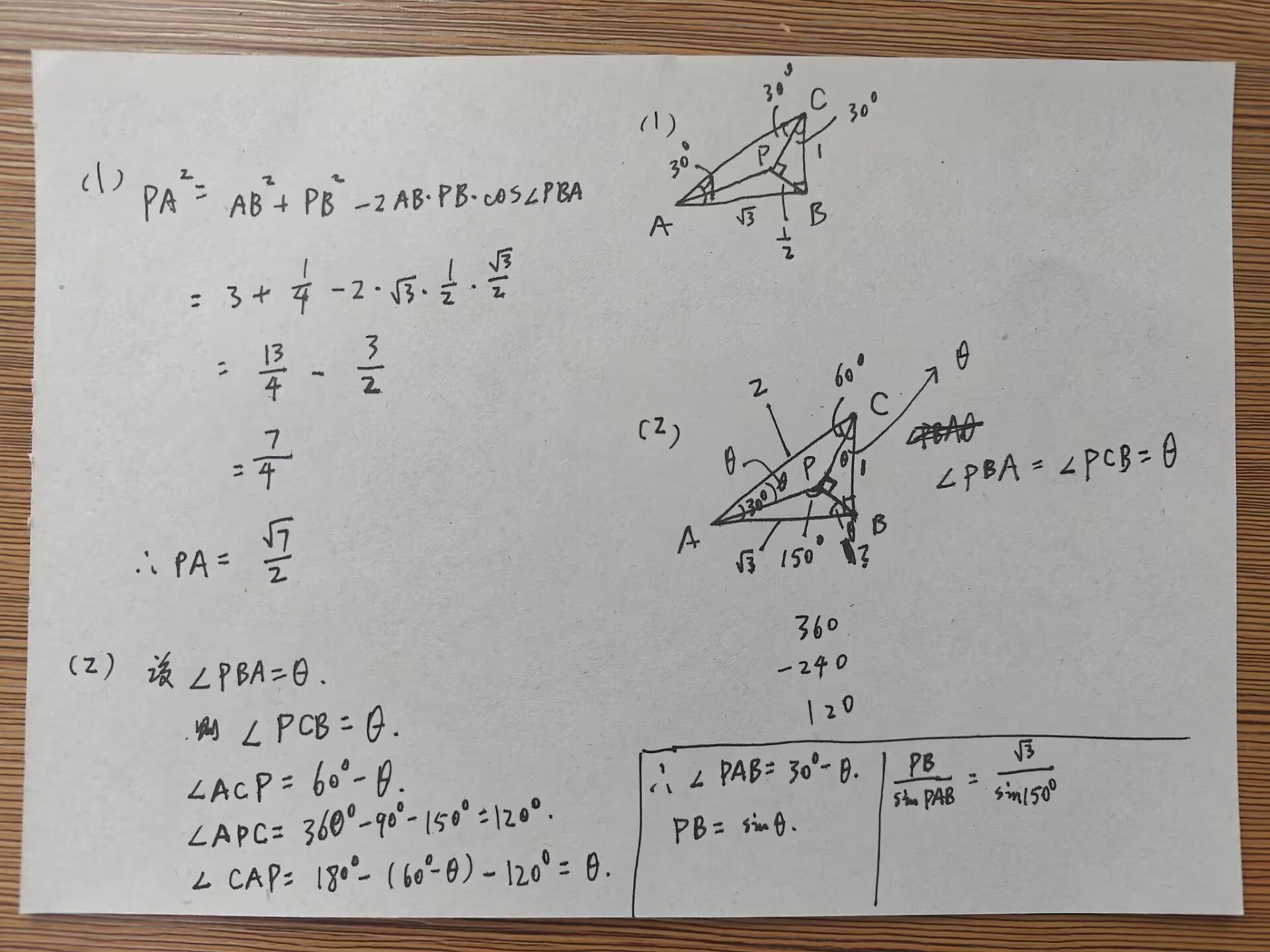
62

解

63

解

64

TIP

倒推法。目标转换法。

箭头指向的方向，表示推出。

较难的题的流程：

使用目标转换法中，倒推过程被假设已知的量在后面又用到了，

这样就会形成多组方程，然后求解。

TIP

对于解三次、高次方程，必须是通过因式分解，将式子一边变为 0，然后令每个因式为 0，解出解。

解出的解要进行验证！

解

65

解

TIP

几等分点结论，权重交叉相乘。

66

解

TIP

大边对大角，如果在一个三角形中，一个角对的边比其他边小，那么这个角一定是锐角。因为如果为钝角就会有 2 个钝角，不可能。

67

解

TIP

求 $b^2+2c^2$ 的最大值，转换为三角函数，求其最值。

比如利用正弦定理进行边角互换，$\frac{a}{sinA}=\frac{2}{sin{60}^{\circ }}=\frac{4}{\sqrt{3}}=\frac{b}{sinB}=\frac{c}{sinC}$

$b=\frac{4\sqrt{3}}{3}sinB,c=\frac{4\sqrt{3}}{3}sinC$

68

解 法一，设两个未知数，并运用互补角余弦相加等于 0 技巧

解 法二，通过几等分点结论解决。

互补角余弦相加等于 0 技巧

注意是相加，不是相等，也不是相减！！

69

解

70

解

TIP

• 更好的方法是用正弦定理表示边，这样就不需要分类讨论开根号后的符号。
• 更好的方法是用正弦定理表示边，这样就不需要必须挖掘出 $\theta$ 必须满足 $0<\theta <\frac{\pi }{2}$ 的隐藏条件。因为当 $\theta >\frac{\pi }{2}$ 时，D 点就在半圆外了

71

解

72

解

TIP

在三角形中，一个式子中，若全是 $a^2,b^2,c^2,...$ 字母，突然出现了一个数字。

这个数字就可能是某条边长。然后可以边角互换。

TIP

三角形中，出现角的倍数关系，一般用正弦进行转换。$A=2B$

则 $sinA=sin2B$

73

解

TIP

两个角互补，除了用余弦定理，还可以用正弦定理。

74

解

TIP

圆内有内接四边形，四边形的对角一定是互补的。

相当于说，圆内的一根弦所对的两个圆顶角，它们是互补的。

除此之外，判定四边形也是通过这个条件来得出的。

75

解

TIP

• 除了这个方法，还可以尝试用三角万能公式。
• 根据条件，其实可以得出四点共圆
• 注意求角的范围，要在每个三角形中都满足

76

解

TIP

两个数的平方和为一个定值，一般使用三角换元。（比万能公式通用一些。）

77

解

TIP

第一问，证明：

若 $C+\frac{B}{2}=\pi$, 则 $C+\frac{B}{2}=A+B+C$

$\frac{B}{2}+A=0$（舍去）

TIP

• 另一种方法是用边长来表示三角形，看起来更简单一点。
• 求 $S=\frac{sin3\theta }{cos\theta }$ 的最值，是比较难求的。因为求导比较复杂，最后最初的最值不是整数，极值点也不是整数。所以一般让求极值点

解析

结论

78

解

见解析

79

解

见解析

80

解

见解析