解三角形的公式总结

正弦定理

$2R=\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$

余弦定理

$c^2=a^2+b^2-2abcosC$

$cosC=\frac{a^2+b^2-c^2}{2ab}$

辅助角公式

对于有任何像这样的式子 $Asin\alpha +Bcos\alpha$，

都可以变成一个正弦函数 $\sqrt{A^2+B^2}sin(\alpha +\beta )$，这样就可以方便的看出这个函数的值域。

恒等式

化简公式

不同角

正弦

$sin(A+B)=sinAcosB+cosAsinB$

$sin(A-B)=sinAcosB-cosAsinB$

sin 内的符号与展开后的符号一样。里加，展开后就是加，里减，展开后就是减。

余弦

$cos(A+B)=cosAcosB-sinAsinB$

$cos(A-B)=cosAcosB+sinAsinB$

cos 内的符号与展开后的符号相反。里加，展开后就是减；里减，展开后就是加。

正切

$tan(A+B)=\frac{tanA+tanB}{1-tanA\cdot tanB}$

$tan(A-B)=\frac{tanA-tanB}{1+tanA\cdot tanB}$

正切展开后的分子与 tan 内的符号相同。展开后的分母与 tan 内的符号相反。

TIP

利用正切两倍角公式，可以快速求两条直线的夹角。

比如直线 1 的斜率为 $k_1$，直线 2 的斜率为 $k_2$，那么它们的夹角 $\theta$ 的正切为

$tan\theta =tan({\theta }_2-{\theta }_1)$

$=\frac{k_2-k_1}{1+k_1{k}_2}$

-

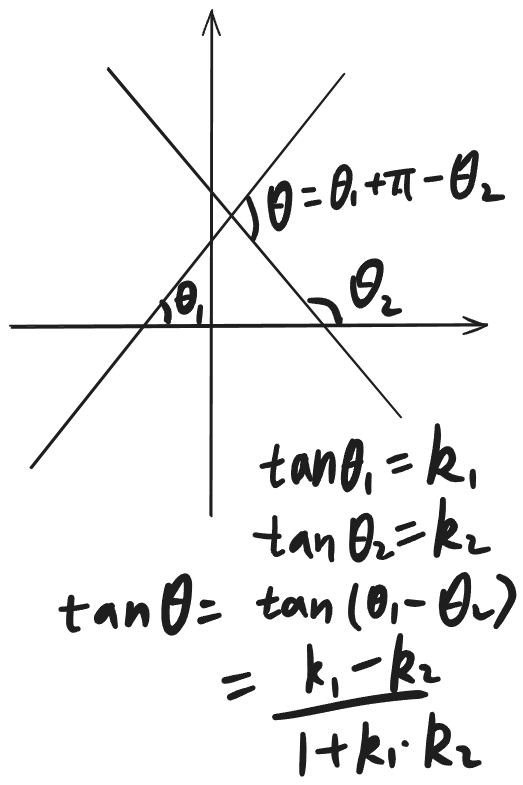但是需要注意，求出的 $tan\theta$ 需要自己判断符号的正负。

积化和差

记忆技巧

都有一个共同点，式子右边都有 $\frac{1}{2},(\alpha +\beta ),(\alpha -\beta )$。

不同的是

1. $sin,sin$ 第一个公式，式子右边都是负号，其余两个公式右边都是正号

2. $sin,cos$ 右边都是 $sin,sin$，其余两个公式右边都是 $cos,cos$

$sin\alpha \cdot sin\beta =-\frac{1}{2}[cos(\alpha +\beta )-cos(\alpha -\beta )]$

$sin\alpha \cdot cos\beta =\frac{1}{2}[sin(\alpha +\beta )+sin(\alpha -\beta )]$

$cos\alpha \cdot cos\beta =\frac{1}{2}[cos(\alpha +\beta )+cos(\alpha -\beta )]$

和差化积

由积变和差公式推导而来。

记忆技巧

$sin=\mathrm{帅}，cos=\mathrm{哥}，sin=\mathrm{嫂}$

只有 sin 和 sin 的加减。只有 cos 和 cos 的加减。

没有 sin 和 cos 的加减。

$\mathrm{帅}+\mathrm{帅}=\mathrm{帅}\mathrm{哥}$

$\mathrm{帅}-\mathrm{帅}=\mathrm{哥}\mathrm{帅}$

$\mathrm{哥}+\mathrm{哥}=\mathrm{哥}\mathrm{哥}$

$\mathrm{哥}-\mathrm{哥}=\mathrm{负}\mathrm{嫂}\mathrm{嫂}$

最后注意式子右边的系数 2 和 $\frac{\alpha +\beta }{2}$ 和 $\frac{\alpha -\beta }{2}$。

积化和差式子右边的系数为 $\frac{1}{2}$，角为 $\alpha +\beta$ 和 $\alpha -\beta$

$sin\alpha +sin\beta =2sin\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2}$

$sin\alpha -sin\beta =2cos\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta }{2}$

$cos\alpha +cos\beta =2cos\frac{\alpha +\beta }{2}cos\frac{\alpha -\beta }{2}$

$cos\alpha -cos\beta =-2sin\frac{\alpha +\beta }{2}sin\frac{\alpha -\beta }{2}$

同角

恒等式

$si{n}^2\alpha +co{s}^2\alpha =1$

正弦二倍角公式

$sin2\alpha =2sin\alpha cos\alpha$

余弦二倍角公式

$cos2\alpha =co{s}^2\alpha -si{n}^2\alpha$

$cos2\alpha =1-2si{n}^2\alpha$

$cos2\alpha =2co{s}^2\alpha -1$

$si{n}^2\alpha =\frac{1-cos2\alpha }{2}$

$co{s}^2\alpha =\frac{1+cos2\alpha }{2}$

正切二倍角公式

$tan2\alpha =\frac{2\tan \alpha }{1-ta{n}^2\alpha }$

例题

例题 1