Java 中的数组的常见算法
数值型数组的特征值统计计算
这里的特征值涉及到:平均值、最大值、最小值、总和等。
数组统计:求总和、均值
/**
* Description:
*/
public class TestArrayElementSum {
public static void main(String[] args) {
int[] arr = {4,5,6,1,9};
// 求总和、均值
int sum = 0; // 因为 0 加上任何数都不影响结果
for(int i=0; i<arr.length; i++){
sum += arr[i];
}
double avg = (double)sum/arr.length;
System.out.println("sum = " + sum);
System.out.println("avg = " + avg);
}
}求数组元素的总乘积
/**
* Description:
*/
public class TestArrayElementMul {
public static void main(String[] args) {
int[] arr = {4,5,6,1,9};
// 求总乘积
long result = 1;// 因为 1 乘以任何数都不影响结果
for(int i=0; i<arr.length; i++){
result *= arr[i];
}
System.out.println("result = " + result);
}
}求数组元素中偶数的个数
/**
* Description:
*/
public class TestArrayElementEvenCount {
public static void main(String[] args) {
int[] arr = {4,5,6,1,9};
// 统计偶数个数
int evenCount = 0;
for(int i=0; i<arr.length; i++){
if(arr[i]%2==0){
evenCount++;
}
}
System.out.println("evenCount = " + evenCount);
}
}求数组元素的最大值
/**
* Description:
*/
public class TestArrayMax {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 1, 9};
// 找最大值
int max = arr[0];
for (int i = 1; i < arr.length; i++) { // 此处 i 从 1 开始,是 max 不需要与 arr[0] 再比较一次了
if (arr[i] > max) {
max = arr[i];
}
}
System.out.println("max = " + max);
}
}找最值及其第一次出现的下标
/**
* Description:
*/
public class TestMaxIndex {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 1, 9};
//找最大值以及第一个最大值下标
int max = arr[0];
int index = 0;
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
index = i;
}
}
System.out.println("max = " + max);
System.out.println("index = " + index);
}
}找最值及其所有最值的下标
/**
* Description:
*/
public class Test13AllMaxIndex {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 1, 9, 9, 3};
//找最大值
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (arr[i] > max) {
max = arr[i];
}
}
System.out.println("最大值是:" + max);
System.out.print("最大值的下标有:");
//遍历数组,看哪些元素和最大值是一样的
for (int i = 0; i < arr.length; i++) {
if (max == arr[i]) {
System.out.print(i + "\t");
}
}
System.out.println();
}
}** 子数组和最大值 **
输入一个整形数组,数组里有正数也有负数。 数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。 求所有子数组的和的最大值。要求时间复杂度为 O(n)。
例如:输入的数组为 1, -2, 3, -10, -4, 7, 2, -5,和最大的子数组为 3, 10, -4, 7, 2,因此输出为该子数组的和为 18。
一个数,加正数会越大,加负数会越小。正数一定比负数大。
/**
* Description:
*/
public class ArrSumMax {
public static void main(String[] args) {
int[] arr = new int[]{1, -2, 3, 10, -4, 7, 2, -5};
int i = getGreatestSum(arr);
System.out.println(i);
}
public static int getGreatestSum(int[] arr) {
int greatestSum = 0;
if (arr == null || arr.length == 0) {
return 0;
}
int temp = greatestSum;
for (int i = 0; i < arr.length; i++) {
temp += arr[i];
if (temp < 0) {
temp = 0;
}
if (temp > greatestSum) {
greatestSum = temp;
}
}
// 处理全是负数的情况,找出负数的最大值
if (greatestSum == 0) {
greatestSum = arr[0];
for (int i = 1; i < arr.length; i++) {
if (greatestSum < arr[i]) {
greatestSum = arr[i];
}
}
}
return greatestSum;
}
}求平均分
分析以下需求,并用代码实现:
(1)在编程竞赛中,有 10 位评委为参赛的选手打分,分数分别为:5,4,6,8,9,0,1,2,7,3
(2)求选手的最后得分(去掉一个最高分和一个最低分后其余8位评委打分的平均值)
public class ArrPinjunFen {
public static void main(String[] args) {
int[] scores = {5, 4, 6, 8, 9, 0, 1, 2, 7, 3};
int max = scores[0];
int min = scores[0];
int sum = 0;
for (int i = 0; i < scores.length; i++) {
if (max < scores[i]) {
max = scores[i];
}
if (min > scores[i]) {
min = scores[i];
}
sum += scores[i];
}
double avg = (double) (sum - max - min) / (scores.length - 2);
System.out.println("选手去掉最高分和最低分之后的平均分为:" + avg);
}
}数组元素的赋值与数组复制
除
一个数组,让数组的每个元素去除第一个元素,得到的商作为被除数所在位置的新值。
public class ArrCalculate3 {
public static void main(String[] args) {
int[] arr = new int[]{12, 43, 65, 3, -8, 64, 2};
// for(int i = 0;i < arr.length;i++){
// arr[i] = arr[i] / arr[0];
// }
for (int i = arr.length - 1; i >= 0; i--) {
arr[i] = arr[i] / arr[0];
}
//遍历 arr
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}随机数
创建一个长度为 6 的 int 型数组,要求数组元素的值都在 1-30 之间,且是随机赋值。同时,要求元素的值各不相同。
TIP
在方法上面加上 @Test,这样就可以直接运行该方法。前提需要导入相应包,比如 JUnit。
import org.junit.Test;
public class RandomTes {
// 5-67 Math.random() * 63 + 5;
@Test
public void test1() {
int[] arr = new int[6];
for (int i = 0; i < arr.length; i++) { // [0,1) [0,30) [1,31)
arr[i] = (int) (Math.random() * 30) + 1;
boolean flag = false;
while (true) {
for (int j = 0; j < i; j++) {
if (arr[i] == arr[j]) {
flag = true;
break;
}
}
if (flag) {
arr[i] = (int) (Math.random() * 30) + 1;
flag = false;
continue;
}
break;
}
}
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
// 更优的方法
@Test
public void test2() {
int[] arr = new int[6];
for (int i = 0; i < arr.length; i++) {// [0,1) [0,30) [1,31)
arr[i] = (int) (Math.random() * 30) + 1;
for (int j = 0; j < i; j++) {
if (arr[i] == arr[j]) {
i--;
break;
}
}
}
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}扑克牌
遍历扑克牌。
提示:使用两个字符串数组,分别保存花色和点数,再用一个字符串数组保存最后的扑克牌。
String[] hua = {"黑桃","红桃","梅花","方片"};
String[] dian = {"A","2","3","4","5","6","7","8","9","10","J","Q","K"};public class Pukepai {
public static void main(String[] args) {
String[] hua = {"黑桃", "红桃", "梅花", "方片"};
String[] dian = {"A", "2", "3", "4", "5", "6", "7", "8", "9", "10", "J", "Q", "K"};
String[] pai = new String[hua.length * dian.length];
int k = 0;
for (int i = 0; i < hua.length; i++) {
for (int j = 0; j < dian.length; j++) {
pai[k++] = hua[i] + " " + dian[j];
}
}
for (int i = 0; i < pai.length; i++) {
System.out.print(pai[i] + " ");
if (i % 13 == 12) {
System.out.println();
}
}
}
}回形数
从键盘输入一个整数(1~20) ,则以该数字为矩阵的大小,把 1, 2, 3 … n*n 的数字按照顺时针螺旋的形式填入其中。
例如:输入数字 2,则程序输出:
1 2
4 3输入数字 3,则程序输出:
1 2 3
8 9 4
7 6 5输入数字 4, 则程序输出:
1 2 3 4
12 13 14 5
11 16 15 6
10 9 8 7import java.util.Scanner;
public class Luoxuanjuzheng {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("请输入一个整数:");
int i1 = scanner.nextInt();
int[][] luoxuannums = getLuoxuannums(i1);
for (int i = 0; i < luoxuannums.length; i++) {
int[] rowArr = luoxuannums[i];
for (int j = 0; j < rowArr.length; j++) {
if (rowArr[j] > 9) {
System.out.print(rowArr[j] + " ");
} else {
System.out.print(rowArr[j] + " ");
}
;
}
;
System.out.println("");
}
;
}
public static int[][] getLuoxuannums(int num) {
int[][] arr = new int[num][num];
// 代表左刻度
int left = 0;
// 最右边数的刻度
int right = num - 1;
// 代表最顶数的刻度
int top = 0;
// 代表最底部数的刻度
int bottom = num - 1;
int count = 1;
// 每一圈是一个循环
while (left <= right) {
// 左 -> 右
for (int i = left; i <= right; i++) {
arr[top][i] = count++;
}
// 上 -> 下
for (int i = top + 1; i <= bottom; i++) {
arr[i][right] = count++;
}
// 左 <- 右
for (int i = right - 1; i >= left; i--) {
arr[bottom][i] = count++;
}
// 上 <- 下
for (int i = bottom - 1; i >= top + 1; i--) {
arr[i][left] = count++;
}
left++;
right--;
top++;
bottom--;
}
return arr;
}
}数组元素的反转
数组对称位置的元素互换。
法一:arr.length / 2
public class ArrSwap1 {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5};
System.out.println("反转之前:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
// 反转
/*
思路:首尾对应位置的元素交换
(1)确定交换几次
次数 = 数组.length / 2
(2)谁和谁交换
for(int i=0; i<次数; i++){
int temp = arr[i];
arr[i] = arr[arr.length-1-i];
arr[arr.length-1-i] = temp;
}
*/
for (int i = 0; i < arr.length / 2; i++) {
int temp = arr[i];
arr[i] = arr[arr.length - 1 - i];
arr[arr.length - 1 - i] = temp;
}
System.out.println("反转之后:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}法二:left < right
public class ArrSwap2 {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5};
System.out.println("反转之前:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
// 反转
// 左右对称位置交换
for (int left = 0, right = arr.length - 1; left < right; left++, right--) {
//首 与 尾交换
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
System.out.println("反转之后:");
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}数组的扩容与缩容
数组的扩容
题目:现有数组 int[] arr = new int[]{1,2,3,4,5};,现将数组长度扩容 1 倍,并将 10, 20, 30 三个数据添加到 arr 数组中,如何操作?
public class Arrkuorong {
public static void main(String[] args) {
int[] arr = new int[]{1, 2, 3, 4, 5};
int[] newArr = new int[arr.length << 1];
for (int i = 0; i < arr.length; i++) {
newArr[i] = arr[i];
}
newArr[arr.length] = 10;
newArr[arr.length + 1] = 20;
newArr[arr.length + 2] = 30;
arr = newArr;
//遍历 arr
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}数组的缩容
题目:现有数组 int[] arr={1,2,3,4,5,6,7}。现需删除数组中索引为 4 的元素。
public class Arrsuorong {
public static void main(String[] args) {
int[] arr = {1, 2, 3, 4, 5, 6, 7};
// 删除数组中索引为 4 的元素
int delIndex = 4;
// 方案 1:
/* // 创建新数组
int[] newArr = new int[arr.length - 1];
for (int i = 0; i < delIndex; i++) {
newArr[i] = arr[i];
}
for (int i = delIndex + 1; i < arr.length; i++) {
newArr[i - 1] = arr[i];
}
arr = newArr;
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
} */
// 方案 2:
for (int i = delIndex; i < arr.length - 1; i++) {
arr[i] = arr[i + 1];
}
arr[arr.length - 1] = 0;
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}数组的元素查找
顺序查找
顺序查找:挨个查看。
要求:对数组元素的顺序没要求。
查找 value 第一次在数组中出现的 index。
public class TestArrayOrderSearch {
public static void main(String[] args) {
int[] arr = {4, 5, 6, 1, 9};
int value = 1;
int index = -1;
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value) {
index = i;
break;
}
}
if (index == -1) {
System.out.println(value + "不存在");
} else {
System.out.println(value + "的下标是" + index);
}
}
}二分查找
注意
二分法查找要求此数组必须是有序的!
public class Arrerfen {
public static void main(String[] args) {
int[] arr3 = new int[]{-99, -54, -2, 0, 2, 33, 43, 256, 999};
boolean isFlag = true;
int value = 256;
// int value = 25;
int head = 0; // 首索引位置
int end = arr3.length - 1; // 尾索引位置
while (head <= end) {
int middle = (head + end) / 2;
if (arr3[middle] == value) {
System.out.println("找到指定的元素,索引为:" + middle);
isFlag = false;
break;
} else if (arr3[middle] > value) {
end = middle - 1;
} else { // arr3[middle] < value
head = middle + 1;
}
}
if (isFlag) {
System.out.println("未找打指定的元素");
}
}
}数组元素排序
排序的定义
假设含有 n 个记录的序列为 {R1, R2, ..., Rn},其相应的关键字序列为 {K1, K2, ..., Kn}。将这些记录重新排序为 {Ri1, Ri2, ..., Rin},使得相应的关键字值满足条件 Ki1 <= Ki2 <= ... <= Kin,这样的一种操作称为排序。
通常来说,排序的目的是快速查找。
衡量排序算法的优劣
- 时间复杂度:分析关键字的比较次数和记录的移动次数
常见的算法时间复杂度由小到大依次为:
空间复杂度:分析排序算法中需要多少辅助内存
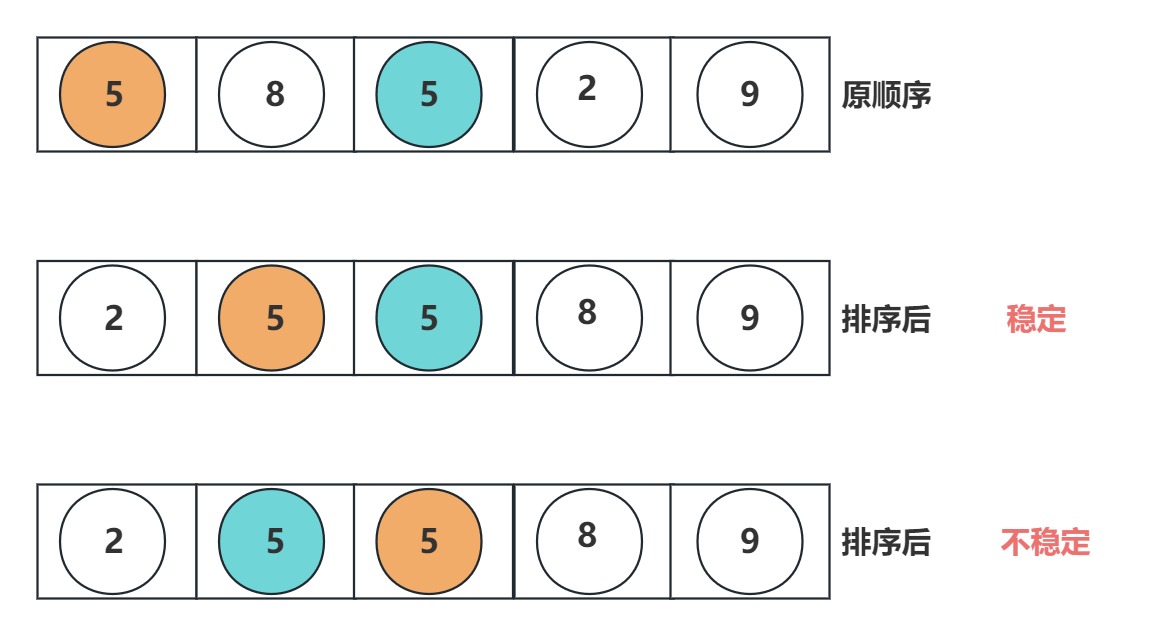
稳定性:若两个记录 A 和 B 的关键字值相等,但排序后 A、B 的先后次序保持不变,则称这种排序算法是稳定的
排序算法分类
内部排序和外部排序。
- 内部排序:整个排序过程不需要借助于外部存储器(如磁盘等),所有排序操作都在内存中完成。
- 外部排序:参与排序的数据非常多,数据量非常大,计算机无法把整个排序过程放在内存中完成,必须借助于外部存储器(如磁盘)。外部排序最常见的是多路归并排序。可以认为外部排序是由多次内部排序组成。
十大内部排序算法
数组的排序算法很多,实现方式各不相同,时间复杂度、空间复杂度、稳定性也各不相同:
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | 稳定 | ||||
| 希尔排序 | 不稳定 | ||||
| 选择排序 | 不稳定 | ||||
| 堆排序 | 不稳定 | ||||
| 冒泡排序 | 稳定 | ||||
| 快速排序 | 不稳定 | ||||
| 归并排序 | 稳定 | ||||
| 计数排序 | 稳定 | ||||
| 桶排序 | 稳定 | ||||
| 基数排序 | 稳定 |
冒泡排序
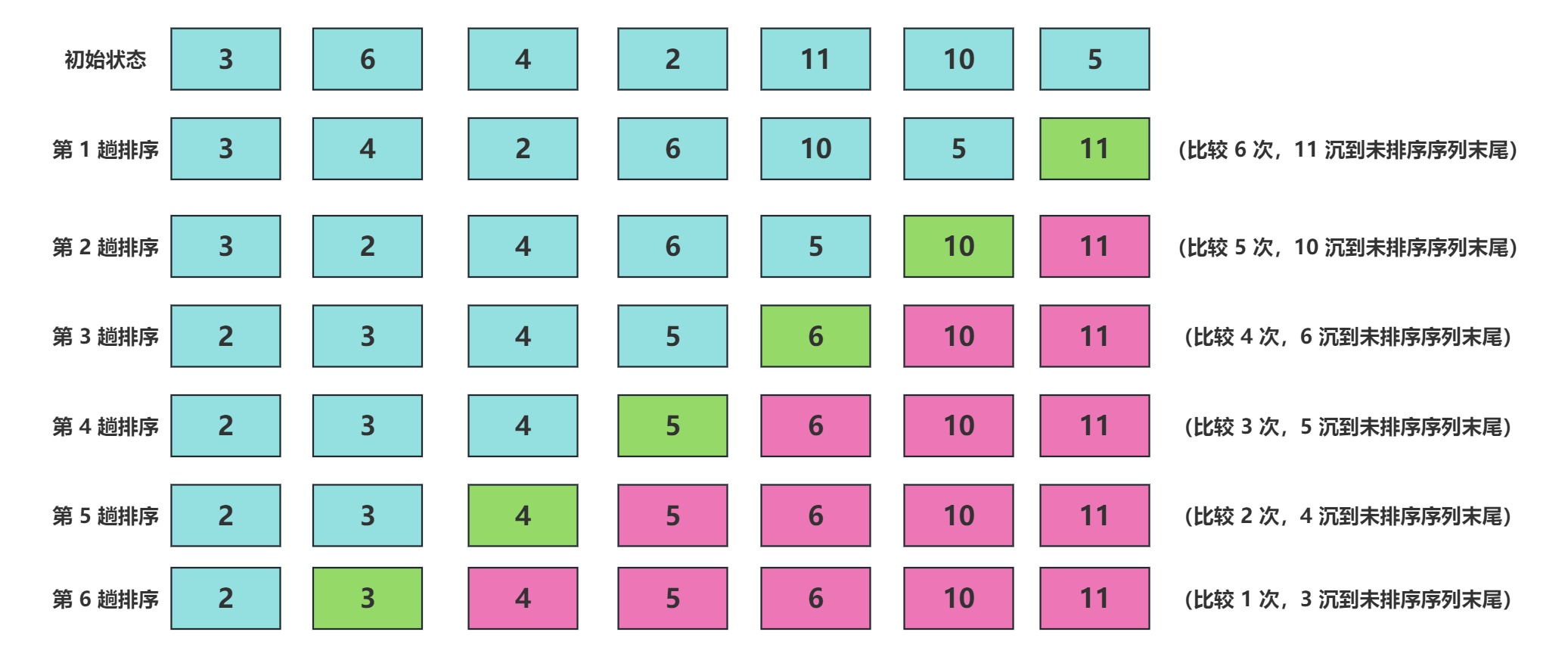
排序思想:
- 比较相邻的元素。如果第一个比第二个大(升序),就交换他们两个。
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较为止。
public class TestBubbleSort1 {
public static void main(String[] args) {
int[] arr = {3,1,2,5,4};
bubbleSort(arr);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
public static int[] bubbleSort(int[] arr) {
// 会循环 arr.length - 1 次
// 不会走刻度 0。会走刻度 1 ~ arr.length - 1
for(int i = arr.length - 1; i > 0; i --) {
for (int j = 0; j < i; j ++) {
int pre = arr[j];
int next = arr[j + 1];
if (pre > next) {
arr[j + 1] = pre;
arr[j] = next;
}
}
}
return arr;
}
}优化版冒泡排序:
public class TestBubbleSortOptimize {
public static void main(String[] args) {
int[] arr = {12,2,3,3,4,5,3,1,2,5,4};
bubbleSort(arr);
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
public static int[] bubbleSort(int[] arr) {
// 会循环 arr.length - 1 次
// 不会走刻度 0。会走刻度 1 ~ arr.length - 1
boolean isBubbleOk = true;
for(int i = arr.length - 1; i > 0; i --) {
for (int j = 0; j < i; j ++) {
int pre = arr[j];
int next = arr[j + 1];
if (pre > next) {
arr[j + 1] = pre;
arr[j] = next;
isBubbleOk = false;
}
}
if (isBubbleOk) {
// 退出循环
break;
}
}
return arr;
}
}快速排序
快速排序(Quick Sort)由图灵奖获得者 Tony Hoare 发明,被列为 20 世纪十大算法之一,是迄今为止所有内排序算法中速度最快的一种。 快速排序的时间复杂度为
快速排序通常明显比同为
排序思想:
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
- 递归的最底部情形,是数列的大小是零或一,也就是永远都已经被排序好了。虽然一直递归下去,但是这个算法总会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。

内部排序性能比较与选择
性能比较
- 从平均时间而言:快速排序最佳。但在最坏情况下时间性能不如堆排序和归并排序。
- 从算法简单性看:由于直接选择排序、直接插入排序和冒泡排序的算法比较简单,将其认为是简单算法。对于 Shell 排序、堆排序、快速排序和归并排序算法,其算法比较复杂,认为是复杂排序。
- 从稳定性看:直接插入排序、冒泡排序和归并排序时稳定的;而直接选择排序、快速排序、Shell 排序和堆排序是不稳定排序。
- 从待排序的记录数 n 的大小看,n 较小时,宜采用简单排序;而 n 较大时宜采用改进排序。
选择
- 若 n 较小(如 n≤50),可采用直接插入或直接选择排序。
- 当记录规模较小时,直接插入排序较好;否则因为直接选择移动的记录数少于直接插入,应选直接选择排序为宜。
- 若文件初始状态基本有序(指正序),则应选用直接插入、冒泡或随机的快速排序为宜。
- 若 n 较大,则应采用时间复杂度为
的排序方法:快速排序、堆排序或归并排序。
